
avant le big bang Big Bang 10-43 s 10-35 s
d'après
sciences et avenirs Hors série Mars 96 : "Comprendre l'infini"
et d'après le site http://www.iap.fr/Documentations/Cosmologie/PLS.html
|
|
|
|
avant le big bang Big Bang 10-43 s 10-35 s |
|
dernière mise à jour le:
|
|
menu général perdu? |
aujourd'hui: on part d'une équation mathématique appellée métrique, il s'agit d'une hypothèse de travail . La géométrie de l'univers ( l'étude des courbes géodésiques) et les lois de la physique se déduisent de cette métrique: il s'agit des déductions logiques et de calculs formels indiscutables. Reste alors à mettre une topologie sur ce modèle géométrique et physique: là on retrouve simplement des hypothèses de travail. Nous sommes donc bel et bien dans le domaine des mathématiques. Le choix des hypothèses n'étant pas toujours lié à l'observation ( impossible par exemple d'observer ce qu'il y a à "l'intérieur d'un trou noir ) c'est parfois la religion ou la métaphysique qui dictent alors leur choix.
B A BA de
topologie
En mathématiques une topologie est la donnée d'ensembles ouverts et fermés d'un espace, s'ensuit la notion de voisinages et donc de limite et de continuité
2 espaces ont la même topologie si on peut passer de l'un à l'autre par déformation continue ( autrement dit les familles d'ouverts et de fermés sont les mêmes à une transformation continue près ) par exemple une sphère et un ellipsoide ont la même topologie.
un rectangle replié sur lui même et recollé par les bords à la même topologie qu'un tore ( beignet ) si vous êtes à l'intérieur d'un carré mais si vous arrivez sur un côté vous ressortez par le côté opposé
les 5 polyèdres réguliers servent à représenter certains espaces multiconnexes par exemple considérez l'intérieur d'un cube mais si vous arrivez sur une face vous ressortez par la face opposée, c'est alors la même topologie qu'un hypertore

| dodécaèdre | hexaèdre | tétraèdre | Icosaèdre | Octaèdre |
sciences et avenirs Hors série Mars 96 : "Comprendre l'infini"
les
balbutiements de la cosmologie Géocentrisme
![]()
La notion de cosmos appliquée à
l'organisation de l'univers apparaît ainsi vers le VIe siècle avant
notre ère chez les Milésiens (Thalès, Anaximandre et
autres physiciens de la ville de Milet, en Asie mineure) : la réalité
n'est pas le chaos que décrivait Hésiode dans sa
"Théogonie" , deux siècles plus tôt ; elle est au contraire belle et
arrangée.
le monde était considéré comme étant dans l'espace - par exemple
un cosmos enclos dans le volume d'une sphère, elle-même plongée dans un
espace extra-cosmique infini, sans propriété physique. Chez les
Aristotéliciens, le monde s'identifie à l'espace, et il est fini. Le
soleil et la lune ne sont plus considérés comme des divinités.
|
|
L'histoire de la cosmologie tourne sans cesse autour de la lancinante question : l'espace est-il fini ou infini ? Au VIe siècle avant notre ère règne l'idée d'un Monde (terre, planètes, étoiles) fini, entouré d'un milieu infini. Puis, au IVe siècle, Platon postule dans son dialogue intitulé le Timée que le monde et les cieux étaient tous deux finis, enclos dans une série sphère. Le souci premier de sa modélisation cosmologique est celui d'harmonie et de symétrie maximale (la sphère étant la figure parfaite par excellence, elle doit naturellement s'inscrire dans l'architecture cosmique pour refléter la perfection et l'immuabilité divines). |
Vient alors Aristote ( le fondateur de la dialectique et donc de la logique binaire : énonce le principe du tiers exclus ), qui élimine l'infini de toute la physique, avec une influence qui durera deux millénaires. En passant de l'infini au fini et en identifiant le monde physique à un espace géométrique, les aristotéliciens accomplissent la première étape clef de la modélisation cosmologique. Le monde est fini et clos par la dernière sphère céleste le temps est lui en revanche infini la Terre est au centre ( système géocentrique entourée de 7 sphères. Le monde est fini parce qu'il est parfait. Selon Aristote: le dieu premier moteur fait tourner le monde de toute éternité; il ne peut être qualifié de l'infini, même si sa puissance ( en tant que moteur immobile capable de mouvoir la plus éloignée des sphères célestes) est sans limite
La nature de l'espace fut découverte progressivement. L'idée d'un monde fini, borné par une ultime sphère où auraient été accrochées les étoiles fixes, se maintint jusqu'au temps de Nicolas Copernic.
Le
XVII siècle
Héliocentrisme ![]()
Le XVIIe siècle voit une évolution opposée: les sphères aristotéliciennes éclatent après plusieurs événements
|
Copernic (1473-1543): Héliocentrisme basé sur la relation mathématique entre distance soleil planète et la durée de révolution. |
 |
Né d'un père marchand de Cracovie. Avec son frère aîné, ils se font clercs et poursuivent de longues études qui les mènent à Cracovie, Bologne, Padoue, Rome, Ferrare. Nicolas s'intéresse aux mathématiques, au dessin, au droit canon, à la médecine, et surtout à l'astronomie. C'est cependant en droit canon qu'il obtient son titre de docteur en 1503. Il est réputé comme médecin pendant son séjour à Heilsberg, puis travaille comme administrateur dans l'église et peut-être à la cour. Il écrit alors (1529) un traité sur les finances. Reste attaché par la suite à l'évêché de Frauenburg.
Copernic monte ses premiers observatoires dans les années 1506-1510. Il observe longuement le soleil, la lune et divers planètes et mûrit lentement et discrètement son système héliocentré. Son avis d'expert est réclamé lorsque les autorités écclésiastiques pensent aux premières réformes du calendrier.
Ces amis le poussent à publier mais il s'y refuse, jusqu'à ce qu'un disciple des dernières années, Joachim Rheticus, prenne les choses en main. Celui rencontre beaucoup d'opposition, mais peut fournir à son maître à moitié paralysé une première version complète en 1543. Le jour même, Copernic meurt.
|
les considérations métaphysiques de Giordano Bruno( 1548-1600) il déclare devant l'inquisition : "J'enseigne l'univers infini, effet de la puissance infinie de Dieu" Il s'oppose à Aristote car pour lui l'infini est parfait puisqu'il contient d'innombrables perfections. L'univers n'est pas une création détachée de Dieu mais il participe de l'infinité divine. L'univers n'est pas géocentrique il n'a aucun centre. Il sera brulé en 1600 pour hérésie
|
 |
 |
Famille noble, dont le père
avait des talents reconnus comme musicien et mathématicien. Sa
famille le pousse vers la médecine, mais il choisit les
mathématiques et la mécanique. Il écrit son premier traité en 1588
sur le centre de gravité des solides et obtient un poste à
l'université de Pise. De cette période, il publie sur la chûte des
corps. Mais devant une oppositon de plus en plus forte de la part
des partisans de la physique d'Aristote, il part pour Padoue en
1592. Là, il travaille au thermomètre et surtout au téléscope.
Cette invention ( qui lui est probablement injustement attribuée ) lui permet d'observer les satellites de Jupiter et les phases de Vénus, autant de preuves selon lui de la validité du système Copernicien. Ce qu'il proclame rapidement, haut et fort en dépit d'une puissante opposition. Dans les années suivantes, son énergie semble être absorbée par la lutte avec les autorités ecclésiastiques, alors que, dans le mème temps, Képler met rapidement au point ses trois principes. Galilée doit affronter les partisans de Ptolémée et d'Aristote, mais aussi ceux de Tycho Brahé qui propose un système concurrent de Copernic et plus en vogue, et perd deux procès face à l'inquisition (1616 et 1633). |

| La révolution
copernicienne: le soleil est au centre et la terre
tourne autour son mouvement est causé par le soleil ( gravitation
) elle tourne de plus sur elle même ce qui crée une illusion de
rotation du soleil autour de la terre. En d'autres termes esprit
simple explication simple esprit subtil explication subtile
ou en core pourquoi faire simple quand on peut faire compliqué?. Plus sérieusement la révolution copernicienne consiste à raisonner au lieu de se fier à l'observation "Ne crois pas ce que tu vois": "la raison n'aperçoit que ce qu'elle produit, elle doit prendre les devants et forcer la nature à répondre à ses questions au lieu de se laisser conduire en laisse par elle". |
 |
| les observations de Tycho-Brahé(1546-1601): selon lui l'univers a 2 axes : le soleil tourne autour de la Terre et les autres planètes tournent autour du soleil (1580) |  |
 |
Tycho Brahé
vient d'un famille noble danoise qui le destinait à la diplomatie
mais Tycho préfèra les sciences. Ces intérêts allaient des
mathématiques, à l'astronomie en passant par l'alchimie et
l'astrologie. La couronne danoise lui fournit l'appuie financier nécéssaire pour construire un laboratoire d'alchimie et un observatoire (vers 1580). En 1599, il devint mathématicien attitré du Saint Empire Germanique et résida à Prague. Képler fut alors son assistant. Il mit au point dans ces années son système astronomique avec la Terre au centre avec la lune et le soleil tournant autour d'elle. Les autres planètes étaient des satellites du soleil. Son système avait l'avantage de satisfaire à la plupart des observations de l'époque et de laisser la terre immobile, ce qui allait aussi de soi à l'époque. Son système s'opposait donc au système de Copernic, antérieur de près d'un demi-siècle. |
L'ouvrage de vulgarisation de Thomas Digges
passage du monde clos à l'Univers infini. Cette nouvelle vision cosmologique est consacrée par Newton, qui identifie désormais l'Univers à l'espace euclidien infini. Newton est aussi l'artisan du principe d'équivalence entre la chutte des corps ( équation du premier degré) et le monvement des planètes ( équation du second degré ) regroupés sous un même modèle nommé force de gravitation ( 1687). monde et espace coïncident et sont infinis.
Un autre mauvais procès intenté à la cosmologie est qu'elle ne serait pas assez fondée sur le témoignage des sens. Pourtant, cette caractéristique n'a nullement empêché Copernic de fonder sa nouvelle hypothèse sur une vision purement esthétique de l'univers, en faisant fi des erreurs dont étaient entachées les tables d'observation astronomiques ("Je ne peux qu'admirer ceux qui ont opté pour l'héliocentrisme en dépit du témoignage de leurs sens", dit plus tard Galilée). Et Johannes Kepler de découvrir l'ellipticité des orbites planétaires en se fondant sur la croyance en l'harmonie des sphères.
Curieusement, le terme de cosmologie n'est apparu qu'en 1731, dans l'ouvrage intitulé Cosmologia Generalis du baron allemand Christian Wolff, disciple de Leibniz : depuis deux millénaires et demi il existait donc un discours sur l'univers qui n'avait pas de nom! Wolff, comme la plupart de ses prédécesseurs, s'efforça d'aborder les questions sur la nature physique du monde en se dégageant le plus possible du mythe et de la religion.
Pour de nombreux physiciens, la cosmologie voisinait avec le rêve et l'extase. Les récits "cosmologiques" tels ceux de Platon, Cicéron, Dante ou Cyrano, mettaient en jeu des êtres "exceptionnels" (parler de l'univers comme une totalité, c'est comme se placer extérieur à lui), capables de raconter leur expérience de l'inexpérimentable.
| Relativité |  |
Il est vrai que, jusqu'au début du XXe siècle, les considérations sur l'univers n'étaient étayées par aucune observation proprement cosmologique, de sorte que les modèles étaient plaqués sur des présupposés philosophiques et religieux. Ne croyons pas pour autant que cette interpénétration de la physique et de la philosophie ait cessé : Albert Einstein, l'inventeur de la théorie de la relativité générale, qui sert de base à toutes les études cosmologiques actuelles, s'y est le premier laissé prendre ; parmi les solutions possibles de ses équations, il choisit pour des raisons esthétiques celle qui décrivait un univers statique et fini. De même, on ne peut pas démontrer le "principe cosmologique" qui sous-tend tous les modèles actuels d'univers et stipule qu'il n'existe aucune position privilégiée dans l'espace.
auteur du Principe d'équivalence de l'inertie et de la gravitation consécutif au principe de la relativité restreinte: " dans tout système de Galilée les lois ont la même forme et sont conservées par les transformations de Maxwell.
Principe de la relativité étendu à toute la physique: Les transformations de Galilée sont une approximation des transformations de Lorentz.
introduction de la relativité du temps. Introduction de i dans la métrique de minkowski ds²=dx²+dy²+dz²+dt² devient ds²=-dx²-dy²-dz²+c²dt² il s'ensuit que le principe de Galilée est le mouvement géodésique dans un espace plat ( euclidien) alors que le principe de Newton est le mouvement géodésique dans un espace courbe. Mis en perspective avec une vision d'univers en expansion, l'espace est plat sauf vers certaines limites temporelles ( big bang ou big crunch ) ou géométriques ( trouns noirs)
Dans les modèles cosmologiques relativistes, l'Univers s'identifie à une entité physico-géométrique : l'espace-temps-matière. Remarquons que l'identification du monde physique et de l'espace (ou de l'espace-temps) géométrique reste mal comprise du public. Lorsqu'un conférencier parle de l'expansion de l'Univers, il se voit invariablement poser la question : dans quoi l'Univers gonfle-t-il? Cette formulation incorrecte est sans doute accentuée par l'analogie trop souvent employée entre l'Univers en expansion et la surface d'un ballon que l'on gonfle. En fait, l'Univers ne gonfle dans rien, puisqu'il n'existe pas d'espace en dehors de lui. On ignore souvent, tout comme les Grecs d'il y a deux mille ans, que les mathématiques savent décrire des espaces non euclidiens parfaitement finis (un vaisseau spatial filant droit devant lui reviendrait à son point de départ), mais n'ayant nul besoin d'un espace référent extérieur. De même, le temps, qui est une propriété de l'Univers au même titre que l'espace, n'a pas de référent extérieur, de sorte que l'autre question souvent posée : qu'y avait-il avant le Big Bang, est également incorrecte. Vers 1230, le philosophe Guillaume d'Auvergne l'avait remarquablement exprimé : "De même que le Monde n'a pas de dehors, n'a pas d'au-delà, puisqu'il contient et embrasse toute chose, de même le temps, qui a commencé à la création du Monde, n'a pas d'auparavant ni de précédemment, puisqu'il contient en lui tous les temps qui sont ses parties."
La cosmologie relativiste fait appel aux géométries non-euclidiennes, si bien que, désormais, les deux possibilités d'espace fini ou infini sont envisageables. En effet, les modèles de Big Bang indiquent que l'espace est soit sphérique (de courbure positive), soit hyperbolique (de courbure négative), soit euclidien (de courbure moyenne nulle). Dans le premier cas, des astronomes qui mesureraient la somme des angles de très grands triangles, dans l'espace, trouveraient une valeur supérieure à 180 degrés; dans le deuxième cas cette somme serait inférieure, -à 180 degrés, et c'est seulement dans le troisième cas qu'ils trouveraient la valeur de 180 degrés que nous mesurons sur les feuilles de papier.
La différence se joue dans la quantité moyenne de matière contenue dans l'Univers - puisque, en relativité générale, la matière détermine la géométrie de l'espace-temps. Au-dessous d'un certain seuil critique de densité, l'espace est hyperbolique, au-dessus il est sphérique; c'est seulement à la valeur exacte de la densité critique que l'Univers est euclidien.
A côté de justes critiques, de faux procès sont intentés à la cosmologie. L'un d'entre eux a injustement gâché la renommée scientifique du plus grand cosmologiste de ce siècle : Georges Lemaître, inventeur du concept de big bang avec le russe Alexandre Friedmann. On lui a reproché de vouloir confirmer par la science le récit de la Genèse. Il n'en était rien : abbé, certes, mais brillant scientifique, Lemaître tenait à une distinction radicale entre science et religion, pensant que l'on ne pourra jamais réduire l'Être suprême au rang d'une hypothèse scientifique - comme le disait à Napoléon le mathématicien français Pierre Simon de Laplace.
Les modèles d'Univers de A.Friedmann et G.Lemaître se distinguent par les propriétés de l'espace (telle la courbure) et l'évolution temporelle de l'Univers (expansion ou contraction). Les propriétés de l'espace sont de trois types :
|
|
modèles à courbure positive, telle l'hypersphère à trois dimensions. si l'espace est sphérique, l'Univers est spatialement fini et temporellement "fermé" : après la phase actuelle d'expansion il se contractera et son histoire s'achèvera par l'opposé d'un Big Bang nommé Big Crunch |
| modèle euclidien, où la courbure est nulle et où la somme des angles de tout triangle est égale à 180 degrés. Si l'Univers est euclidien , il est temporellement "ouvert" : son expansion se poursuivra éternellement. Cependant on ne sait plus, dans ce cas, si l'espace est fini ou infini, car la question de la finitude ou de l'infinitude de l'espace relève non plus de la relativité générale, mais de la topologie. | |
| modèles à courbure négative, telle une nappe plissée où chaque point serait analogue à une selle de cheval. Si l'Univers est hyperpolique , il est temporellement "ouvert" : son expansion se poursuivra éternellement. Cependant on ne sait plus, dans ce cas, si l'espace est fini ou infini. |
si k=1 modèle elliptique
si k=0 modèle parabolique
si k=-1 modèle hyperbolique
Ainsi un certain nombre de "variantes" topologiques des espaces à trois dimensions peuvent être appliquées à la description de l'espace réel.
|
|
Un espace hyperbolique compact.
Modèle d'un espace chiffonné hyperbolique. L'intérieur de cet icosaèdre dont les faces de même couleur sont identifiées est un espace fermé de courbure négative (sur la figure, certaines faces visibles à l'avant sont identifiées à des faces cachées à l'arrière). L'espace réel pourrait être de cette nature. C'est l'une des possibilités qu'explorent les cosmologistes aujourd'hui. |
Avec ces possibilités de "fermeture" topologique de l'Univers disparaît une croyance récente de la cosmologie moderne, selon laquelle, pour savoir si l'espace est fini ou infini, il suffirait de mesurer la quantité de matière qu'il contient. On voit simultanément réapparaître, par le détour de mathématiques sophistiquées, un mythe ancien : l'usage des corps parfaits platoniciens pour expliquer l'architecture secrète du monde !
Ces considérations apportent également un nouvel éclairage sur les rapports entre le monde "réel" et le monde "perçu". Le monde perçu est inévitablement brouillé par l'imperfection de nos sens. La physique nous apprend qu'il existe aussi un brouillage "objectif", reflétant la nature physique du monde indépendamment de nos sens. Au niveau microscopique (quantique), le principe d'incertitude d'Heisenberg implique qu'une particule, comme un électron, n'a de "réalité" que si l'on effectue une mesure sur elle, et cette mesure modifie ses propriétés. Au niveau macroscopique, les "mirages gravitationnels" déforment notre vision de l'Univers. Ceux-ci résultent de la courbure de l'espace-temps. Les rayons lumineux émis par les astres lointains (galaxies, quasars) rencontrent sur leur trajet jusqu'à nous des masses (étoiles, galaxies, amas de galaxies); en courbant l'espace dans leur voisinage, ces masses intermédiaires perturbent les trajets des rayons lumineux et engendrent des illusions d'optiques, des "mirages" qui déforment, amplifient ou démultiplient les images des sources situées à l'arrière-plan.
les
modèles d'Univers chiffonnés: modèles quantiques ![]()
le brouillage cosmique pourrait être complet, et non plus localisé dans certaines directions d'observation. Là, ce serait la forme globale de l'espace qui démultiplierait les trajets de la lumière entre les sources lointaines et nous, de sorte que nous serions plongés dans un univers d'apparence très différente de ce qu'il est en réalité. Par exemple, chaque galaxie "réelle" aurait des dizaines d'images fantômes réparties dans toutes les directions du ciel, mais qu'il serait difficile de reconnaître en tant que telles. L'univers nous paraîtrait vaste, "déplié", contenant des milliards de galaxies, tandis qu'il serait en réalité beaucoup plus petit, chiffonné, contenant beaucoup moins d'objets qu'on n'en voit. Ce miroir-aux-alouettes cosmique plongerait le cosmologiste entre l'illusion de l'infini et une réalité finie.
L'illusion cosmique ( d'après les travaux de JP Luminet CNRS)
 |
On peut envisager l'espace comme
un jeu de Pac Man, où les personnages qui sortent par un bord de
l'écran réapparaissent sur le bord opposé. Cette configuration est
celle d'un tore, puisqu'on obtient un tore en recollant les bords
opposés d'un carré. On peut reprendre cette idée de recollement à trois dimensions : si l'Univers était comme l'intérieur d'une boîte dont les faces opposées étaient recollées, le nombre de galaxies nous paraîtrait bien supérieur à ce qu'il est en réalité. Sur cette figure, on a représenté les résultats d'une simulation où l'on a placé au hasard un vingtaine de galaxies dans un modèle d'Univers "hypertorique" dont la taille est d'un milliard d'années-lumière seulement (a) |
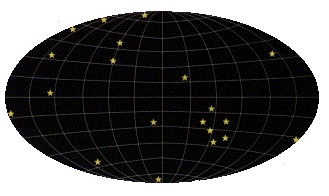 |
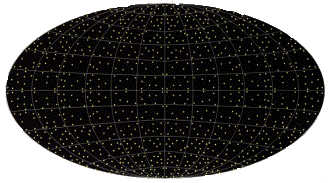
L'aspect du ciel ne se réduit pas aux images des vingt galaxies (b), car les rayons lumineux empruntent de multiples trajets pour nous parvenir. |
 sciences
et avenirs Hors série Mars 96 : "Comprendre l'infini" sciences
et avenirs Hors série Mars 96 : "Comprendre l'infini" |
Au contraire, l'image de chacune des "vraies" galaxies est démultipliée en un grand nombre d'images "fantômes", qui donnent à l'Univers l'apparence d'être beaucoup plus vaste et peuplé (c). |
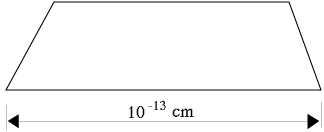
Peut-on légitimement remonter le passé cosmique jusqu'à la singularité ? Non : lorsque les dimensions de la "bulle" d'univers observable (aujourd'hui 10^28 centimètres) étaient inférieures à 10^(-33) centimètre (correspondant, selon les modèles actuels, à un temps plus petit que 10^(-43) seconde), la relativité générale classique perd tout pouvoir prédictif car les effets quantiques deviennent prépondérants : une théorie de la gravitation quantique devient impérative, nécessitant une unification complète des quatre interactions physiques (électromagnétique, forte, faible, gravitationnelle).
Cependant cette théorie n'existe pas, en raison de difficultés fondamentales liées à la nécessaire redéfinition de concepts tels que l'espace, le temps, la causalité, le rôle de l'observateur, etc. De nombreuses propositions ont été faites : supercordes, introduction de dimensions supplémentaires, etc. Ce n'est pas le lieu de les recenser, mais je considérerai l'une des approches, celle de la cosmologie quantique.
La cosmologie quantique résulte de l'application des principes de la mécanique quantique à la description de l'Univers dans son ensemble. Elle tente de répondre de façon rationnelle aux questions des origines (d'où venons-nous ?) et de la contingence (pourquoi y a-t-il quelque chose plutôt que rien?).
La description de la dynamique de l'Univers à l'échelle quantique a initialement été proposée dans les années 1960 par John Wheeler et Bryce de Witt : au niveau microscopique, la géométrie de l'univers devient "floue", comparable à une sorte d'écume constamment agitée de petites fluctuations. La cosmologie quantique ne peut être mise en oeuvre que pour des modèles très simples, ce qui réduit sa portée par rapport aux ambitions théoriques originelles. 2 aproximations principales celle de Hartle et Hawking et celle de Lindé
 |
- un modèle classique (non quantique), où l'espace est lisse à toutes les échelles, |
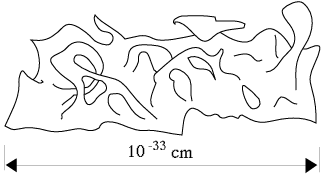 |
un
modèle où la structure à petite échelle est agitée de fluctuations
quantiques,
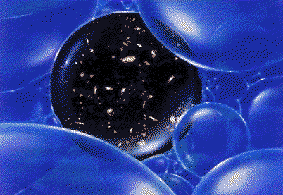
En termes simples, le modèle quantique de Hartle et Hawking n'a ni frontière ni bord, comme la surface d'une sphère mais avec deux dimensions supplémentaires. Autrement dit, l'Univers serait fini non seulement dans l'espace (son "volume" total serait fini) mais aussi dans le temps. La problématique singularité initiale disparaîtrait : l'Univers n'aurait pas eu de commencement et n'aurait jamais de fin. Cependant cette nouvelle "éternité du temps" ne serait trouvée qu'au prix de l'abandon du temps cosmique réel (mesuré par les horloges ou par l'expansion des galaxies) au profit d'un temps imaginaire (au sens mathématique du terme). |
 sciences et avenirs Hors série Mars 96 : "Comprendre l'infini" sciences et avenirs septembre 96 |
un modèle
quantique où l'Univers n'est qu'une bulle au sein d'une mousse
composée d'un nombre infini de bulles, chacune ayant ses propres
lois physiques. L'approche de A. Lindé, bien différente, suppose des conditions initiales chaotiques. Qualitativement, Lindé présente sa solution (non exacte) sous la forme d'un gigantesque univers éternel et auto-reproducteur, constitué d'une "mousse d'Univers". Chaque bulle de cette mousse aurait ses propres caractéristiques : constantes physiques, nombre de dimensions spatiales, dynamique. Notre Univers observable ne serait qu'une infime partie de l'une de ces bulles, démesurément gonflée par l'inflation. Là encore, l'Univers "global" n'aurait ni commencement ni fin, même si les bulles individuelles, avec notamment ce qui semble être "notre univers", pouvaient naître et mourir. |