

Etonnant été 2019, pour une fois ce n'est pas un contenu putassier ou complotiste qui fait le buzz mais un petit calcul mathématique parti d'outre atlantique qui arrive devant mes yeux via mon smartphone : https://hitek.fr/42/probleme-mathematiques-toile-internaute_7010
J'y lis : "Mais dernièrement, sur Twitter, une équation a divisé les internautes. Et pour cause, les participants ne parviennent pas à trouver une réponse commune. L'équation est la suivante : 8 / 2 (2 + 2). "
D'emblée je suis agacé, puisque ceci n'est pas une équation, mais un simple enchainement d'opérations, on peut aussi appeler cela une expression numérique ou une suite d'opérations. Je remarque d'ailleurs que parmi les commentaires les plus nazes le mot "équation" est repris ( forcément j'ai envie de dire).
Plus loin dans l'article je lis que cette écriture porte à confusion et que 2 cas sont possibles, et là je suis profondément heurté, puisque ce que j'ai appris et transmets à mes élèves, c'est que les mathématiques sont une langue universelle et que les règles de priorité sont les mêmes dans le monde entier. Mais je leur apprends aussi que tout résultat, toute règle, toute propriété est unique et que "toute affirmation est soit vraie soit fausse et que toute troisième possibilité est à exclure". c'est le principe du tiers exclus d'Aristote , à la base de la logique dite "binaire" et donc des mathématiques élémentaires ( en particulier les éléments d'Euclide). Il faudra attendre le 20ème siècle pour que certains se lancent dans ce qu'on appelle la logique ternaire : une affirmation peut être soit vraie soit fausse soit indécidable. ( gardez cela à l'esprit pour comprendre mon commentaire du point de vue de Cédric Villani un peu plus bas ainsi que la conclusion)
Enfin je suis terriblement agacé par l'acronyme "PEMDAS"
qui selon l'auteur de l'article est "un
moyen mnémotechnique pour retenir l'ordre des priorités : parenthèses, exposants,
multiplications, divisions, additions, soustractions." Et
là, pim je me dis que très vite les lecteurs ( et l'auteur?) vont penser
que la multiplication est prioritaire sur la division, et que l'addition
est prioritaire sur la soustraction. Or,
ce n'est pas le cas la multiplication et la division sont d'égale
priorité puisque "diviser c'est multiplier par l'inverse" et de même
l'addition et la soustraction sont d'égale priorité puisque "soustraire
c'est additionner l'opposé". Lorsque
les opérations sont d'égale priorité on effectue de gauche en droite
dans le sens de lecture.
Et là, je me prends à pester contre le brillant pédagogue qui a eu l'idée
de cet acronyme pour aider les élèves à ne pas apprendre par coeur (pardon
pour le gros mot) des règles de priorité exprimées in extenso dans
un véritable cours de maths ( pardon encore des gros mots). Pis encore je
me mets à pester contre les brillants pédagogues qui se sont dit que
l'idée du brillant pédagogue était une idée géniale et qui se sont
empressés de l'imiter. Cela provoque bien sur des erreurs que ne
provoqueraient pas l'énoncé des règles in extenso. Voici deux exemples (
mais il y en a plein parmi les commentaires) :


il vient des USA, c'est de là que le buzz est parti. Or pour les anglo saxons le "slash" représente la division, et donc pour nous ce calcul doit être écrit ainsi : 8 : 2 (2 + 2). J'y reviendrai plus loin car de nombreux internautes dans les commentaires affirment que le slash est un trait de fraction, ce qui est vrai à condition de ne pas violer les règles de priorité. Le quotient de 2 nombres peut être écrit :
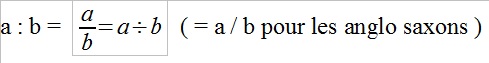

revient donc à décider que la division est prioritaire sur la multiplication ou que la multiplication est prioritaire sur la division, ce n'est donc pas une question de "slash" mais une question de priorité des opérations.
Voici un commentaire très intéressant pour illustrer l'incompréhension qui découle de la notation anglo saxonne :

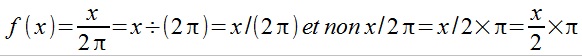
Reste à savoir comment
fonctionnent les anglo saxons. Finalement en écrivant ceci, cela ébranle
mes convictions, au fond les maths ne sont peut-être pas si universelles
que cela.... En tout cas l'ambigüité n'existe pas avec l'écriture
fractionnaire utilisée en France.

Mais
au fait comment les anglo saxons écrivent -ils : deux tiers multiplié
par cinq demis ? parce que ici
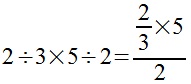
Pour
la deuxième partie du calcul, la multiplication n'est pas écrite ce qui
provoque aussi un florilège de réactions et de confusions. Certains
affirmant même que le résultat est différent selon que la multiplication
est écrite ou non ( on retrouve le même argument sur wikipédia
d'ailleurs , voir plus bas). Ce qui viole totalement le principe du
tiers exclus cité plus haut. la règle est la suivant "on a le droit de ne
pas écrire la multiplication avant ou après une lettre, avant ou
après une parenthèse". Mais
qu'on l'écrive ou non le résultat devra de toutes façons être le
même.
D'aucuns affirment que lorsque la multiplication n'est pas écrite, elle
devient prioritaire sur toutes les autres opérations. J'y vois là une
conséquence de l'enseignement massif de technique stéréotypées et
automatisées pour les fonctions polynomes, mais c'est oublier que
losqu'on écrit 3 + 2x la
multiplication est de toutes façons prioritaire sur l'addition qu'elle
soit écrite ou non. 4 années de pratique automatisée de la 3ème à la
terminale sur les fonctions polynomes a probablement produit cette idée
que 2x est forcément une
entité à part entière et que le 2 et le
x sont indissociables.

Ainsi de nombreux
internautes avancent le fait que dans
8 / 2 (2 + 2) le développement est prioritaire sur
la division, ce qui est faux.
Encore une fois remplacer 2 (2+2) par 2x2+2x2= 4+4=8
revient à considérer que la multiplication est prioritaire sur la
division ce qui est faux.
Il faut noter que la
plupart des internautes qui soutiennent cette vision parlent de
"factorisation" au lieu de parler de "développement"
et l'argument se réplique de commentaire en commentaire avec l'erreur de
vocabulaire associée, ce qui, pardon de le dire , décrédibilise
totalement la véracité de l'argument. Las, décrédibiliser ne veut pas
dire non plus que c'est faux, on peut dire un truc vrai sans le dire de
façon crédible, ou sans donner le bon argument pour le justifier.
Par ailleurs, pourquoi aller développer 2 (2+2) alors qu'on peut
effectuer ce qui est entre parenthèses pour obtenir 2x4 puis ensuite 8 .
Le développement n'a d'intérêt qui si on fait du calcul littéral ou si
cela simplifie le calcul comme par exemple pour calculer 19 ( 100 + 1 )
qui sera plus simple à calculer de tête en développant.
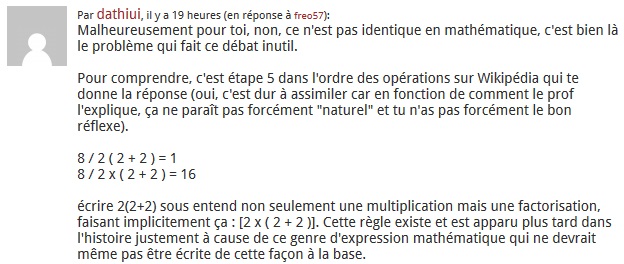
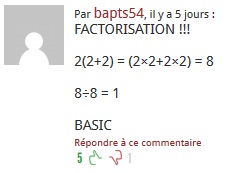
On a vu également des internautes prétendre que le résultat pouvait être différent selon la taille de l'espace qui se trouve avant la parenthèse. S'appuyant sur des calculs de très haut niveau avec des SIGMA. Là franchement on s'égare méchamment. Autant "écraser une mouche avec un rouleau compresseur" comme disait le prof de maths que j'ai préféré pendant mes études. Restons au niveau des maths élémentaires niveau collège. Ici il n'y a pas de SIGMA donc pas d'histoire d'espace.

Tout le monde convient que les parenthèses sont prioritaires et que donc 8 / 2 (2 + 2)= 8 / 2 (4) la question est donc de savoir si ici il faut calculer 8 / 2 x 4 ou 8 / (2 x 4)
On va donc retrouver strictement les mêmes arguments que cité précédemment à savoir que si la multiplication n'est pas écrite elle est prioritaire ( farfelu ça, totalement farfelu, problème de l'enseignement répétitif des polynomes)
soit l'écriture permet les 2 interprétations.

Je suis prof et je trouve 16 ! justement introduire des parenthèses
supplémentaires revient à considérer qu'ici la multiplication serait
prioritaire sur la division
On résume : le "slash" représente la division , "on a le droit de ne pas écrire la multiplication avant ou après une lettre, avant ou après une parenthèse", les parenthèses sont proritaires sur toutes les opérations :
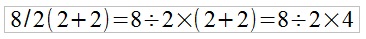




Bien évidemment il ne faut pas se satisfaire des résultats donnés par les machines et ne pas oublier qu'on a ici un simple calcul arithmétique niveau collège, les machines sont programmées par des humains et les humains qui programment les machines ne sont pas des mathématiciens puristes, au mieux ils ont un bon niveau en maths appliquées et en maths de l'informatique. Lorsqu'on sort de l'enseignement supérieur les mathématiques élémentaires sont très loins dans la tête et de nombreux automatismes se sont mis en place, il faut quelques années d'expérience professionnelle d'enseignement pour retrouver les fondamentaux et les enseigner autrement que par "c'est évident" ou "c'est comme ça".En tout cas les machines ne donnent pas toutes la même réponse (cf les nombreux commentaires et l'article de wikipédia ci après, elles ne sont donc pas fiables pour trancher)
Par ailleurs, il est très simple de faire planter une machine à calculer : calculez [111 111 111 111 111 111 111 111 111 111 111 111 111 - 1 ] avec une machine et vous verrez. Ou alors représentez sin(1/x) au voisinage de 0 avec une calculatrice graphique. Les machines sont largement inférieures à l'humain et pour cause, c'est l'humain qui les a fabriquées et programmées.


Comme tous les petits profs de maths que je suis, j'ai un profond respect pour Villani qui est un mathématicien immense, médaille Field vous pensez bien que je ne lui arrive pas à la cheville, c'est évident. Pourtant cela ne signifie pas qu'il a toujours raison. Je ne partage pas son premier point de vue lorsqu'il lui fut demandé pourquoi les jeunes français avaient autant de difficulté en mathématiques ( classés quasi dernier sur les études comparées entre pays de l'OCDE). En effet il répondit alors qu'il fallait enseigner les maths de façon plus ludique et en faisant davantage appel à des problèmes concrets. Or l'école française des mathématiques était la meilleure du monde il y a 30 ans. ET qu'est ce qui a changé depuis? On a éradiqué l'enseignement de la démonstration. Il reviendra finalement lui aussi à ce constat dans le rapport publié à l'été 2018 sur l'enseignement des maths, mais je m'égare.
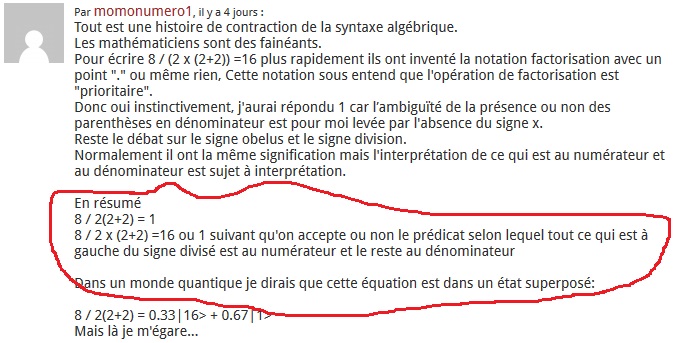
Dans les nombreuses pages web ( à vrai dire tous les sites d'actualité ont publié le leur) traitant de ce buzz j'ai vu passer celui-ci
Voici ce qu'en dit Cédric Villani : aucun résultat n'est valable. "La bonne réaction n'est pas de donner le résultat, dit Cédric Villani. Mais de dire que l'expression est mal écrite et qu'il faut lever l'ambiguïté en ajoutant des parenthèses par exemple." Bref, "mieux vaut partir en vacances sans se casser la tête sur ce problème qui n'en est pas un...".
Je dois donc bien avouer que là je ne sui spas d'accord avec Villani, ça me chagrine car du coup l'argument d'autorité faisant que je suis tout petit face à lui, risque de faire penser au lecteur que j'ai tort. Pourtant l'ambigüité n'a aucune place en mathématiques du moment qu'on se place dans un contexte de logique binaire. voici ce qu'on pourrait dire en logique ternaire ( surement abondamment pratiquée par notre médaille field).
Alors , monsieur Villani je reprends votre propos et je change le
contexte : Je prends une règle de priorité admise de tous, "la
multiplication est prioritaire sur l'addition". et alors il s'en
suit que 2 + 3 x 4 = 2 + 12 = 14. Me direz-vous que l'écriture est ambigüe
et qu'il fallait écrire : 2 + (3 x 4) ? Evidemment non, vous ne direz pas
cela, la règle de priorité est claire.
Et bien cette règle est tout aussi claire : "Lorsqu'il n'y a que des
multiplications et des divisions il faut effectuer les calculs de gauche à
droite". Cette règle est-elle vraie ou fausse? Bien sur elle est vraie.
Elle est alors vraie sans aucune exception, et s'il existait une seule
exception ce serait un contre exemple et alors cette règle serait fausse.
Ou alors, ai-je mal compris la valeur du contre exemple en maths pour
prouver qu'une affirmation est fausse? Si j'ai tort alors on peut jeter
l'axiome du tiers exclus à la poubelle et toute la théorie mathématique
avec puisque cet axiome est à la base de toute démonstration mathématique
( du moins toute la partie binaire d'icelle dont l'arithmétique
élémentaire fait bel et bien partie).
Que l'on suppose que le résultat soit 16 comme je l'ai défendu ou bien que l'on suppose que l'écriture est ambigüe comme le défend Cédric Villani, que penser des internautes qui ont affirmé que le résultat était 1 avec des commentaires "bashing 2.0" ?



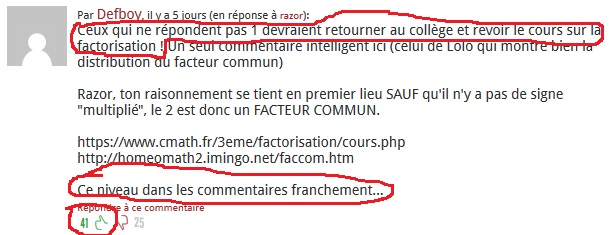
Car il faut bien le dire, le web 2.0 est formidable, ça clashe à tous boûts de champ, certains passent même leur temps à aller dire du mal de telle ou telle célébrité ( on les nomme même les haters). formidable web 2.0 dans lequel tout le monde à un avis tranché sur tout, dans lequel tous les avis de vallent. Dans lequel je viens lacher ma crotte sur un commentaire puis je ne reviens jamais voir comment les autres ont contre argumenté, je zappe je regarde un autre article et je lache une autre crotte. Tout le monde vient poser son commentaire et au bout de 24h l'article est devenu de la préhistoire, tout le monde a zappé sur autre chose. A l'heure où j'écris ces mots, tout le monde se contrefiche certainement de savoir si le résultat est 1 ou 16.
Toutes les répliques d'articles parlant de ce calcul répètent les mêmes erreurs : confusion, entre calcul numérique et équation, confusion entre développement et factorisation, confusion entre moyen mnémotechnique et règle mathématique.
Autre problème, celui qui bashe, qu'il ait raison ou tort récolte plus de réactions positives que de réactions négatives ( voir le comm de defboy ci dessus par exemple). Ce côté "je vote" renforce l'illusion que la majorité aurait raison. Pourquoi pas, si ce sont des problèmes ouverts de société ou de politique ou de philosophie, mais pas pour les mathématiques (Galilée si tu me lis :p ).
Il y a aussi ceux qui assènent sans expliquer, ça aussi c'est très web 2.0
Un petit concentré pour la route : PEMDAS+ Calculatrice + bashing + mauvais résultat :D
